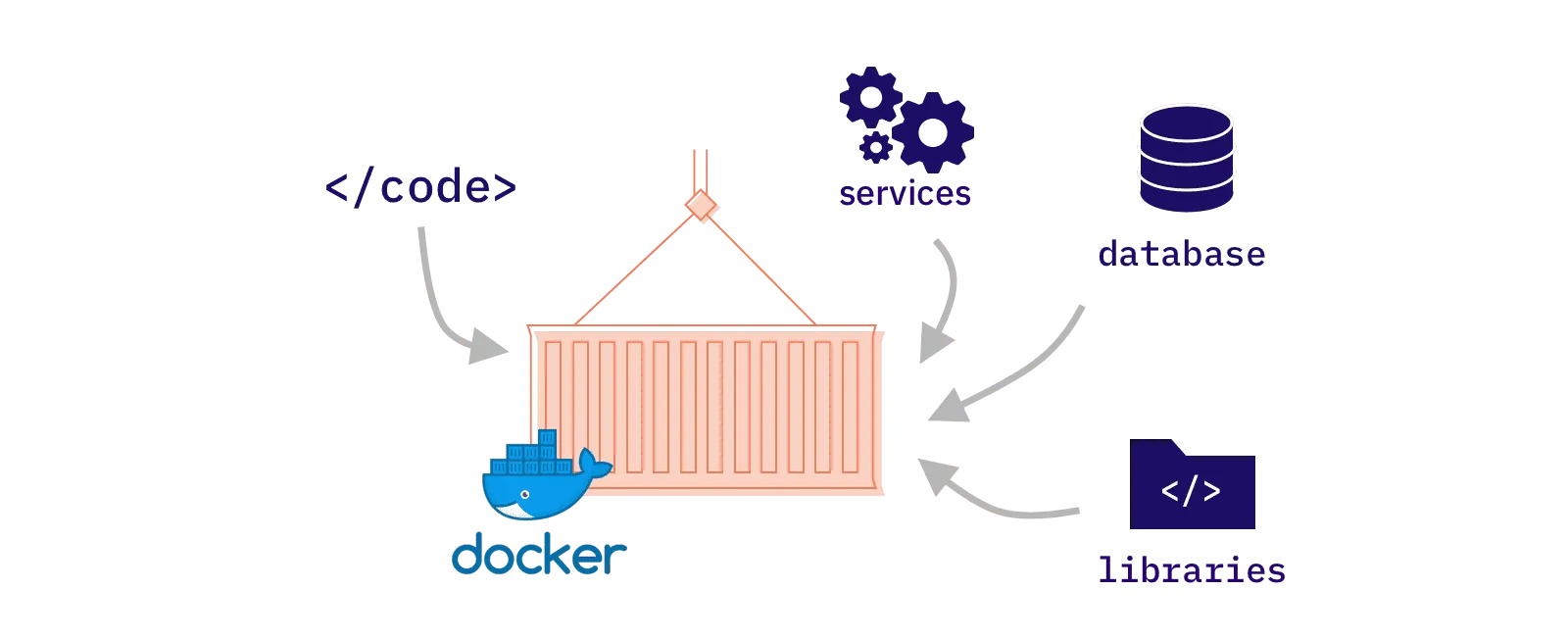
【项目实战】考虑内容的图片缩放
项目报告
项目描述
对于图片缩放,我们希望在缩放时却不影响主体的变换。一般来说,缩放技术有基于离散和连续的两种方法,离散型通常是迭代地寻找一排(或者一列)最小能量的像素,以删除在原图片中无效的像素点;连续型则通过形变等手法改变整个图片的比例。本项目基于Seam Carving [1]和 Image Warping [2]的论文进行代码的复现和结果的比较。
背景
遗传算法
- 进化算法的一种,优化方式属于随机优化
- 受生物遗传算法的启发
- 常用于1. 非连续,非凸,非可微,非线性等难以定义的目标函数 2. 或当搜索空间过大难以使用普通优化方式的问题
过程
- 随机生成一批个体(individual),这一批个体形成了一个群落(population)
- 每个个体其实就是一个解(solution)
- 每个个体具有一个适应度(fitness)的评判值,代表着它对于目标问题的分数
- 根据适应度的高低,高适应度的个体会相互繁衍(crossover)产生后代(下一个个体),并且会进行复制(reproduce)(在迭代中被留下);低适应度的则在下一次进化中被淘汰(discard)
- 在产生个体时,还会有一定的几率发生突变(mutation);突变的发生与适应度无关
- 重复以上的进化过程直到结束
问题描述
在图片缩放问题中,遗传算法中的每个个体就是要找的最小影响的路线,以垂直路线为例: ${s^v}$。为了不改变原图片的结构,我们限制路线的最大跨度不能超过1(即只能在九宫格内移动),可以如下式表示:
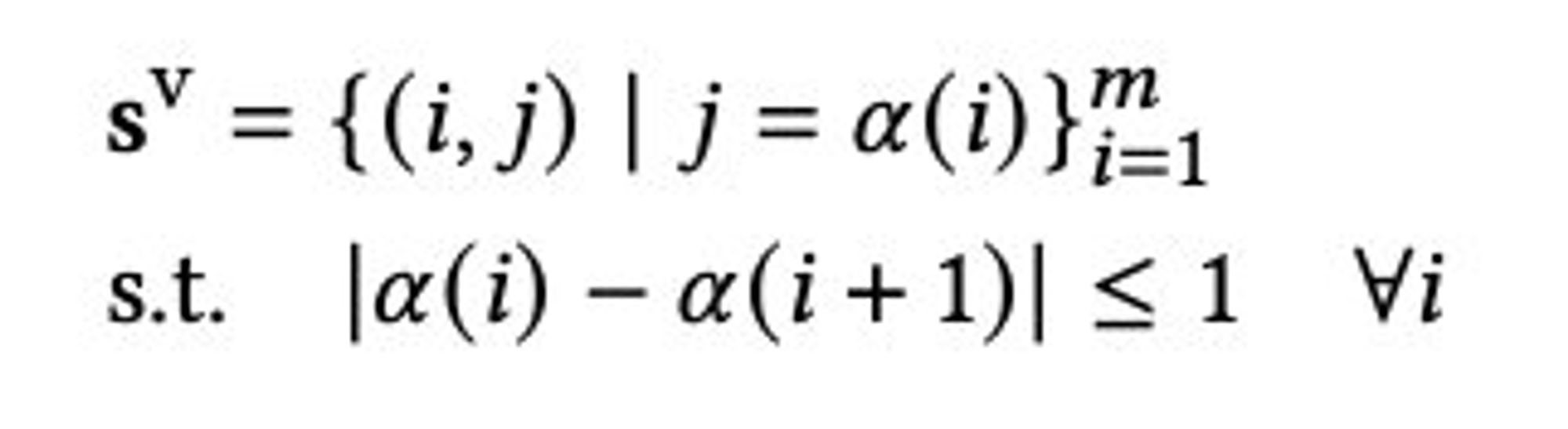
最终我们要寻找的最优路线 ${s^{v*}}$,我们希望它能够达到是图片中影响力最小(能量值最小)的一条路线。即:
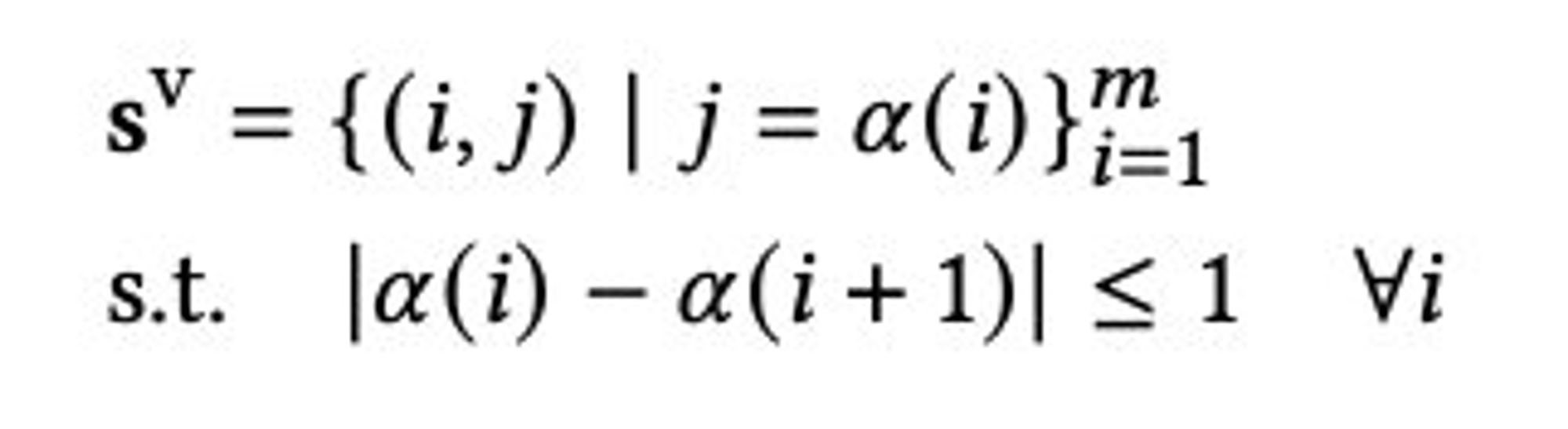
注
:除了遗传算法这种随机算法,我们还要使用动态算法(Dynamic Programming)来解决该问题。由于我们想找到最小能量的路线,因此在探索路线时遵循以下的转换方程式: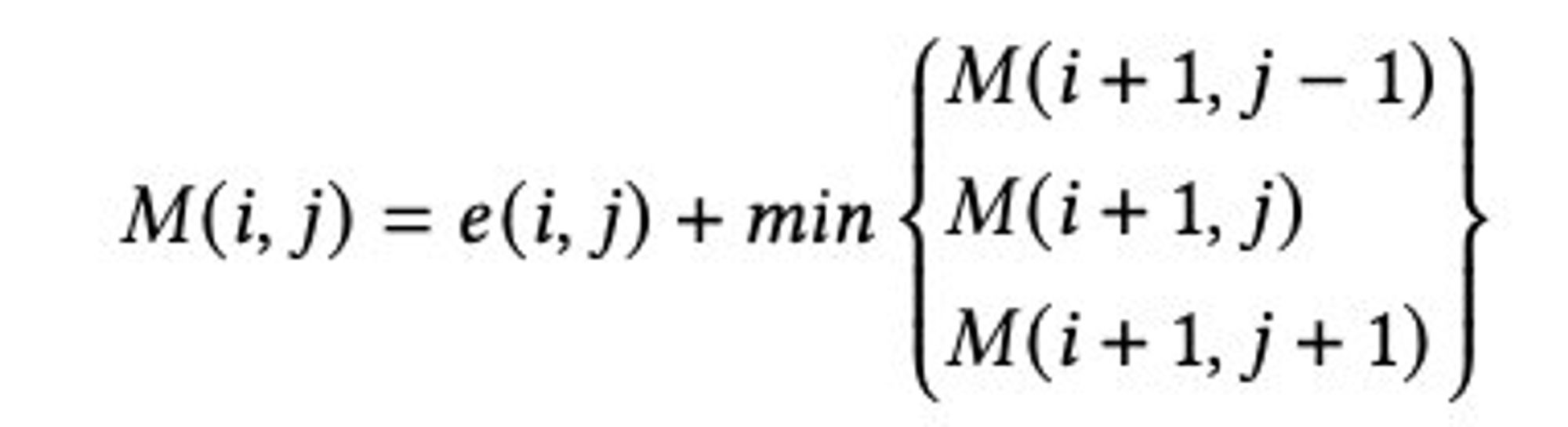
实现过程
- 初始个体:random walk。随机定义一个pivot数作为开始的行i,在这一行随机选取一个点,其他行以[-1,1]为区域进行random walk。
- 复制:当前种群内的前20%的最优个体
- 繁衍:选一个随机数,令两个个体的随机数后的位置对调
- 突变:根据高斯分布对个体的一部分元素进行突变
实验
能量函数(能量图)
尝试了边缘检测和物体的显著性检测两种能量函数并对其进行了比较。
Static Saliency Spectral Residual
模拟注意前视觉搜索的行为。该算法对每幅图像的对数谱进行分析,得到谱残差SR (Spectral Residual)
Static Saliency Fine Grained
该方法基于空间尺度差异计算显著性

Backward
最普通的图片能量计算方式——求偏导。利用有限差分求出gradient maltitude能量图。
Forward
作者认为在寻找Seam的问题中,我们不仅要考虑删除后对原图像的影响(即backward),还要考虑当删除后产生的新的“伪影”的影响。因此Forward的目的是找到产生“伪影”最少的能量图。

最终我们发现Forward和SR的结合得到的能量图效果最好
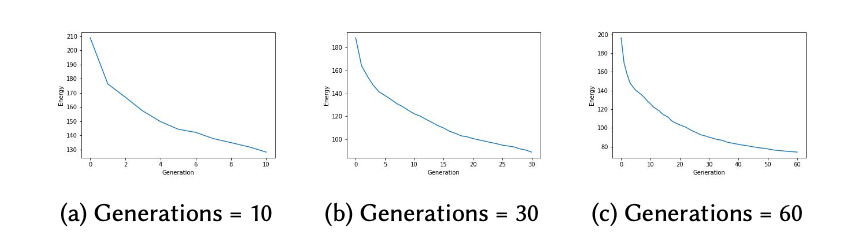
迭代次数
理论上,由于遗传算法属于广域搜索,迭代次数接近无穷时便能得到最优结果。但其缺点也是时间代价过高,如GA方法和warping方法的对比:
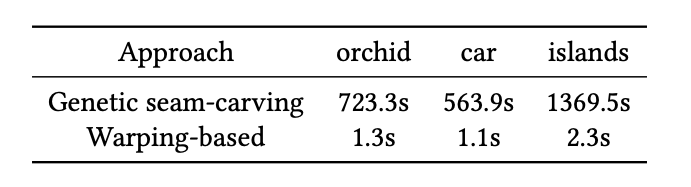
我们也确认了当迭代次数增加时,能量损失会下降更多,效果也会更好

总结
通过对比,我们发现比起warping手法,GA手法确实更容易找到全局最优(体现在GA的结果的图片中更能凸显主体);但是对应的,GA手法耗费时间更长,并且由于是离散算法导致可能出现像素锯齿,影响图片质量。

代码
https://github.com/llsf9/cgo-group-work
参考文献
[1] Saulo AF Oliveira, Francisco N Bezerra, and Ajalmar R Rocha Neto. 2015. Genetic seam carving: A genetic algorithm approach for content-aware image retargeting. In Iberian Conference on Pattern Recognition and Image Analysis. Springer, 700–707.
[2] Yu-Shuen Wang, Chiew-Lan Tai, Olga Sorkine, and Tong-Yee Lee. 2008. Optimized scale-and-stretch for image resizing. In ACM SIGGRAPH Asia 2008 papers. 1–8.