凸优化问题
\text{minimize }f_0(x)\text{subject to } f_i(x)\le 0, i=1...mh(x)=0, i=1...p
目标函数(objective f)必须为凸(convex)
不等式(inequality constraint f)约束函数必须为凸
等式约束函数必须为仿射(affine)
定义域是m个凸的下水平集($f_i(x)$)和p个超平面($h(x)$)的交集
我们其实是在一个凸集上极小化一个凸的目标函数
局部最优解自动成为全局最优解
最优值与最优解 optimal value and optimal point最优值为最优解对应的y值
最优值定义为
p^*=inf\{f_0(x)|满足约束条件\}
当没有可行点(没有点满足约束条件)时,p为不可行(infeasible)且等于$\infty$
如果$p^*=-\infty$,则称这个问题无下界(unbounded below)
当$x^{*}$可行并且$f_0(x^*)=p^{*}$时称之为最优解
凸集合与凸函数
1. convex sets1.1 Line segmentation 直线分割y=\theta x_1+(1-\theta)x_2y=x_2+\theta(x_1-x_2)
$\theta$=1时$y=x_1$,=0时反之,所以称为直线分割
根据式2也可以看做是以x_2为基准。向x_1-x_2延伸的一条线
1.2 affine sets仿射集C上的任意两点连成的直线属于C即
{\theta x_{1}+(1-\theta) x_{2} \in C, \quad \forall x_{1}, x_{2} \in C, \text { and } \theta \in \mathbb{R}}扩展到多点上为
x_1, x_2 ... x_k \in C\bf{AND} {\theta}_1+{\theta}_2+...+{\theta}_k=1\bf{THEN} \theta x_{1}+...+\theta_k x_{k} \in C其中,对于属于C的子空间是$V=C-x_0=\{x-x_0|x\in C\}$
意味着标量乘积之和是闭合的
子空间维数=仿射集维数
1.3 affi ...
最小二乘问题
最小二乘(LEAST-SQUARES)问题定义${f_0(x)=||Ax-b||^2_2 =\sum_{i=1}^k({a_i}^Tx-b_i)^2}$
2-范数${||x||_2=(x,x)^{1/2}=\sqrt{\sum_{i=1}^n x_i^2}}$
最小二乘法上面的式子可被简化为:${(A^TA)x = A^Tb}$${x = (A^TA)^{-1}A^Tb}$代入原式并求hesse矩阵的话${\nabla^2 ||Ax-b||^2_2=2A^TA}$→ 变成了确认 ${2A^TA}$的正定值与否的问题
补充:最小二乘
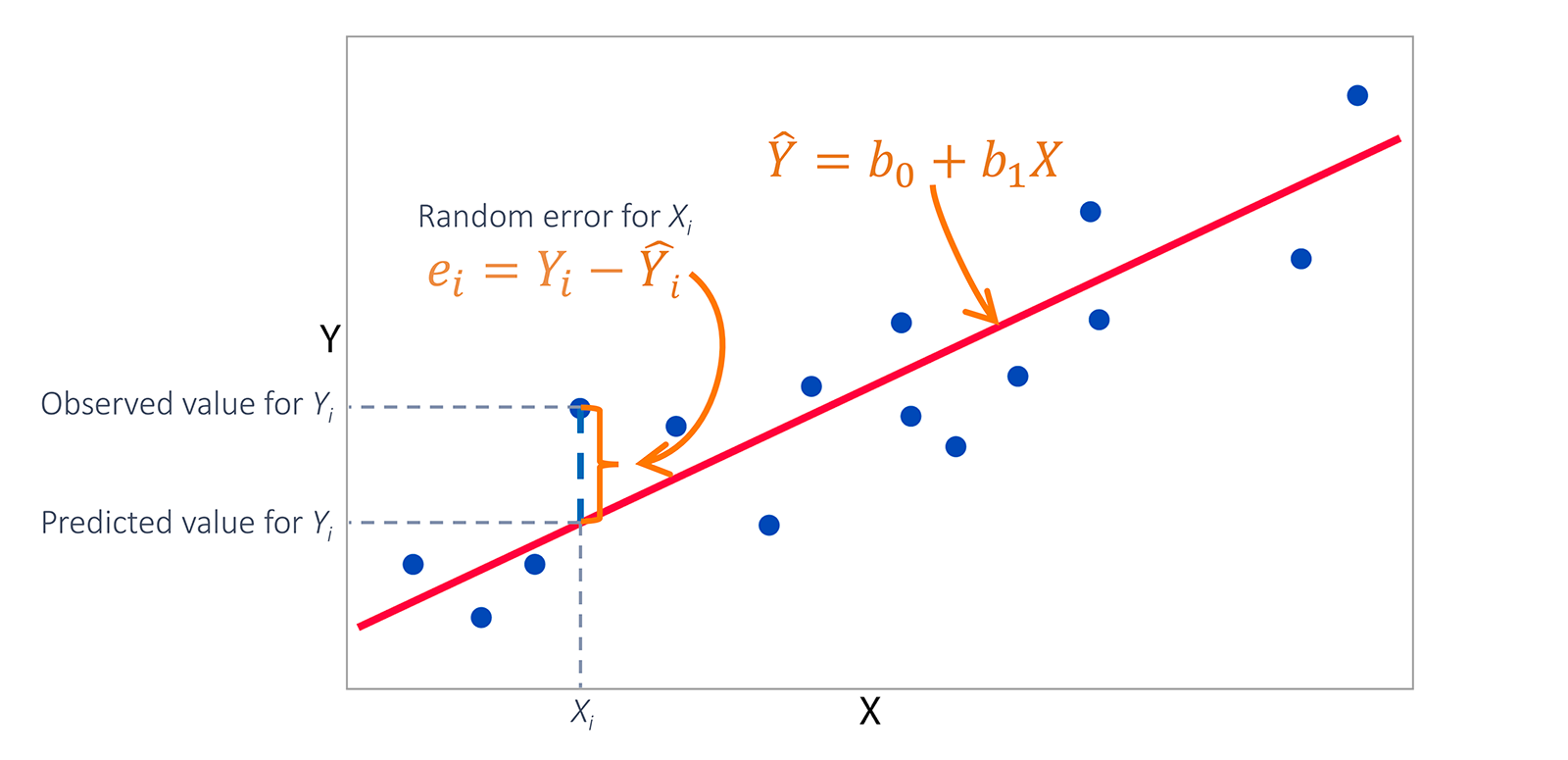
如下二维平面图中有很多个点,假设我们想用一条直线来拟合数据,即期望能找到一条直线能最好地穿过这些数据点。
一个点就可以构造一个方程,而未知数显然只有两个(直线的斜率和截距),因此这就是一个超定系统,我们是没有办法找到一条完美的直线,使得上述的点都在直线上。因此,我们只能期望找到一条最好的“适配(best fitting line)”直线来拟合这些数据
有x作为自变量,y表示x对应的真实值,$y^hat$表示由拟合直线对应的预测值
找一条直线 ...
闲谈-关于美术馆拍摄的变形问题
前几天去艺术馆拍了不少喜欢的画作,本想回来美美做墙纸之类的,结果….
除去我摄影水平不够导致的没有完美对齐的问题,和红框相比能明显看出来似乎加了鱼眼效果般突出来了点
镜头变形
“对于一般的风景画,没有多少直线,对枕形变形不太敏感;但要是以建筑为主体,或者是有较多靠近画框边缘的直线的抽象画,枕形变形就会比较扎眼。如果要把画框拍出来,平直线条紧贴着画面边缘,枕形变形特别容易显出来,佳能红圈20-70/2.8都压不住,慢说任何小数码相机了。这是拍摄绘画的“不利条件”。“
球差(球面収差)透过镜头外侧的光和透镜片中心(近轴)附近的光,因为焦点位置不同而产生变形。原理上来说,只要镜头为球面镜头这一现象就不可避免。相反,球面收差可以通过使用适当设计——非球面镜头来消除。所以,最近的镜头中非球面镜头开始被普遍使用。
题外话物理学的稀巴烂所以基本还停留在初中学的“凸透镜光线汇聚成一点”,所以其实理解这个费了好大的功夫。一些关于为什么与教科书不同,凸透镜的焦点并不能完美汇聚于一点的补充如下:
聚集到一点,需要几个因素1、理想平行光2、理想凸透镜3、理想单一频率4、理想粒子特性(实际上光具有波粒两相 ...
HexoTags
Note{% note [class]%}Any content (support inline tags too.io).{% endnote %}
空白
default
primary
success
info
warning
danger
Mermaid使用mermaid标籤可以绘製Flowchart(流程图)、Sequence diagram(时序图 )、Class Diagram(类别图)、State Diagram(状态图)、Gantt(甘特图)和Pie Chart(圆形图),具体可以查看Mermaide文档
Tabs{% tabs test1 %}<!-- tab -->**This is Tab 1.**<!-- endtab --><!-- tab -->**This is Tab 2.**<!-- endtab -->
表格1表格2这是1这是2
label{% label 我是 %}{% label 什么 blue % ...
无约束最优化
1. Minizer
全局最小值 Global Minizer
局部最小值 Local Minizer
weak
strict
孤立的局部最小值isolated local minimizer 对于凸函数,局部最小值立即成为全局最小值
2. 局部最小值条件
一阶必要条件(FIRST-ORDER NECESSARY CONDITIONS)
函数$f(x)$在点$x^*$可微
梯度${\nabla f(x^*)=0}$
二阶必要条件
满足一阶
hesse矩阵${\nabla^2 f(x^*)}$半正定
海塞矩阵半正定值海塞矩阵的半正定值半正定值:
对于所有x不等于0,都有 ${x^TAx≥0}$
且对某个x不等于0,有 ${x^TAx>0}$
因为hesse矩阵是对称矩阵所以有以下性质:(仅限于对称矩阵!!)半正定:所有特征值都大于等于0正定:所有特征值都大于0负定:所有特征值都小于0
现在虽然知道了确认某点是否为最小值的算法,但是对于如何找到这个点我们还无从得知(总不能把所有点都算一遍吧)
3. 直线探索策略 line search strategy ...
【项目实战】基于跨域学习的行人重识别
pdflink
基于域学习的行人重识别项目描述偏工业项目。主要针对解决公交车的出入口行人重识别课题,来达到自动判断乘客的乘车区间的目的。难点有三:1. 本数据集的出入口的摄像机种类不同(RGB和近红外线) 2. 为保护隐私分辨率较低无法使用面部特征 3. 外部光照影响较大。数据集来源为日本公交公司。
基本思路难点的关键在于我们无法使用过去的方法:颜色特征和面部特征。因此解决的关键是实现提取颜色光照无关的特征(更深层的特征,或域无关的特征)。考虑了以下三种解决方法:
利用深度网络学习域无关特征(DANN,AGW)
手动提取域无关特征(HeadReID)
姿态估计(TODO)
DANN [1]
在一般的分类预测期以外加上了域分类器,以提高特征的抽象度。我们希望提取出的特征无法被域分类器成功判别,以确认生成的特征是域无关的。
AGW [2]
考虑到表层特征差异大的问题,还尝试了通过分开卷积层的方法。首先使用域单独的卷积层提取出表层特征,再进入相同的Resnet+NoLocal块的网络,增加对全域特征的提取能力。
HeadReID
根据文献 [3],仅仅是头部特征也有惊人的表达能力。因此 ...
CSS总结
一 基础属性连接css
内联式<p style="color:red;font-size:12px;">...</a>
嵌入式<style type="text/css"> a{ color:red; font-size:12px; }</style>
外部式<link href="base.css" rel="stylesheet" type="text/css">
一般写在head
优先级:内联式 > 嵌入式 > 外部式
选择器1. 基本选择器
标签选择器:选出所有相同的标签。但无法差异化选择。
:star: 类选择器:class。最常用的选择器。多个元素可以用一个class,一个元素也可以有多个class
多类名
<div class="red font20"></div>
可以在同个class属性中写多个类名,但中间要用空 ...
HTML总结
“标签存在的意义不仅是他们呈现出来的样式,而是让浏览器更好的阅读”
共通标签HTML骨架<html> <head>...</head> <body>...</body></html>
\<html\>\</html\>称为根标签,所有的网页标签都在\<html\>\</html\>中。
\<head\>标签用于定义文档的头部,它是所有头部元素的容器。头部元素有\<title\>、\<script\>、\<style\>、\<link\>、 \<meta\>等标签,头部标签在下一小节中会有详细介绍。
在\<body\>和\</body>标签之间的内容是网页的主要内容,如\<h1>、\<p>、\<a>、\<img>等网页内容标签,在这里的标签中的内容会在浏览器中显示出来。
列表
ul…li无序列表。
< ...
JavaScript总结
《JavaScript DOM编程艺术》
第二章 准备2.1 准备工作
插入方法1.将js代码放到文档<head>中的<script>标签中<head> <script>
2.放到文档最后,</body>之前(推荐:能使网页加载更快)
<script>标签中已经不需要传统的type=”text/javascript”。因为默认即为js。
2.2 语法2.2.3 变量1.变量的声明var mood;2.变量的赋值mood=13;
2.2.4 数据类型
js是弱类型语言,因此不需要声明变量的数据类型。以下的数据类型的变量的声明和赋值语法均相同。
1.字符串(单引号和双引号均可)2.数值3.布尔值(false或true。不需要引号)4.数组
声明1.var sue=Array();2.var sue=[];
赋值1.var sue=Array("a", "b", "c");2.var sue=["a", "b&quo ...