Diffusion model 总结
从去年diffusion的崛起陆陆续续的看了很多文章和应用,也有在自己的研究上加入一些元素。但是浑浑噩噩下来其实对于dm的历史以及进化过程很是浅显, 笔记也非常零碎,借此文章对笔记进行一些整理
符号
T:定量。确定的时间步长。
t:变量。对应的时间步。
生成模型
生成模型的根本其实就是:将训练数据和生成数据的分布尽可能接近
如果将一个个的sample看做是一个个人类,那么控制的参数则有性别,年龄,身高,器官的大小……这些数据的分布情况都决定了AI创造的的新种族是否与人类相似。如果这个种族的平均身高只有120,那必然怎么看都只能算侏儒群体。
将两个数据的分布靠近的方法可以分为下面两类:
- 直接计算:
- 严密计算:Flow-based
- 使用易于计算的上限值计算:VAE,diffusion
- 间接达成
- GAN
在两种方法中,以GAN为首的间接达成的方法曾经一直是主流。其通过增加分辨器的方式进行对抗学习,”逼迫“生成器必须提取非常抽象的特征以生成无法被识别出来真假的sample。但是它的缺点是不够精细,生成样本的质量参差不齐。最近以Diffusion为主的直接计算法又再次登上舞台,但是只要尝试后就知道其在某些领域的生成能力和总体的消耗时间其实仍不如GAN,这也是目前对diffusion优化的方向之一(优化模型,提高泛化能力[Diffusion models beat GANs on image synthesis])
Diffusion Model
前言
首先DM在做的事情其实就是**基于扩散模型的学习过程。**扩散模型是指马尔科夫过程,也就是将一段一段的迁移过程直接用一个式子概括的定理。DM整个过程都基于这个定理。
DM的学习和生成过程可以用下面这张看烂的图概括
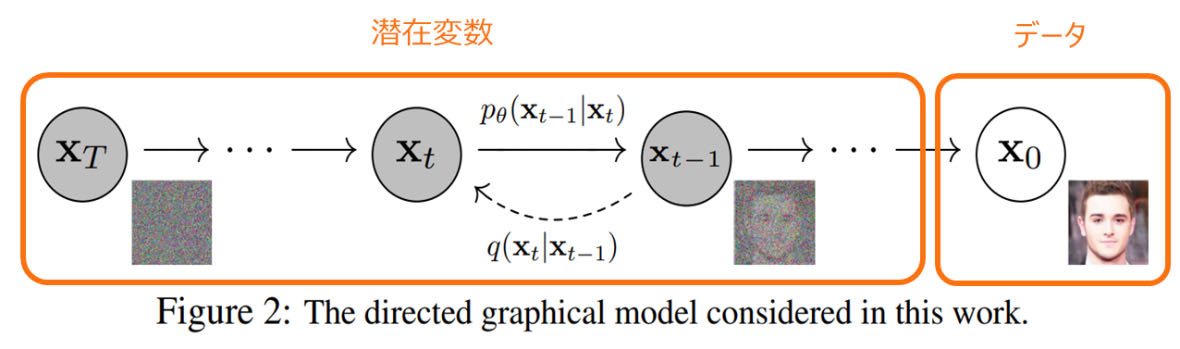
学习过程(Forward process):0到T的过程。从原图片变成遵循高斯分布的噪声。记为q。
训练过程(Reverse process):T到0的过程。从噪声变成图片。记为p。
X0始终代表原始图片,之后的Xt都是从原图片提取出来的特征也好变量也好的东西。
学习过程
单个一小步的过程的迁移概率如下:
${q(X_t|X_{t-1})=\mathcal N(X_t;\sqrt{1-\beta_t}X_{t-1},\beta_tI)}$
根据马尔科夫定理,将所有迁移过程汇总为如下的一个式子
${q_\theta}(X_{1:T}|X_0) = \prod^T_{t=1}q(X_t|X_{t-1})$
可以看到,里面其实只有一个参数beta。这个beta也是定好的,会随着定义好的schedular线性或者对数改变,在代码中一般定义为beta_schedular。因此在整个学习过程中没有需要学习的参数。
一些思虑:
Xt究竟用什么表示?我们只定义了迁移过程的概率式,但是Xt究竟用什么表示呢?
应该是在学习过程就定死的。学习过程相当于外部添加噪声的过程,这个噪声通常是由随机函数产生,因此这个是已知量。
训练过程
首先我们假设学习过程中最终生成的噪声图片遵循平均值0分布为1的正态分布(可能通过什么转换变成的)
${p(X_T)=\mathcal N(0,I)}$
每一步的去噪过程可被表述为与加噪过程相同的形式。不同的是,这里的平均值和分布不再是之和beta相关的定值,而是需要DNN进行学习的未知参数。
${p_\theta(X_{t-1}|X_t)=\mathcal N(X_{t-1};\mu_\theta(x_t,t), \Sigma_\theta(x_t,t))}$
z最终整个过程被表现为
${p_\theta(X_0:T)=p_{\theta}(X_t)\prod^T_{t=1}p_\theta(X_{t-1}|X_t)}$
其实我还是没有太搞懂。概率的过程和最终的生成同样图片的关联在哪里。
Diffusion Models Beat GANs on Image Synthesis 中的解释

……在高层面来说,扩散模型其实就是通过一个反转的加噪过程,来对分布进行采样。这个过程从Xt持续到X0。不同的时间步t对应不同的噪声等级。对于每个Xt可以看做是X0和一个与t成比例的噪声e混合而成的数据。其中在本文中,我们假设e是从高斯分布中提取出来的。
但是这个去噪的过程是很复杂的。虽然DM很牛掰但是也不可能一下子就学会整个过程。就像人画东西也需要一个部位一个部位的画,而DM需要一个层次一个层次的画。所以DM的整个创作过程是由无数个简单的创作过程组成的。
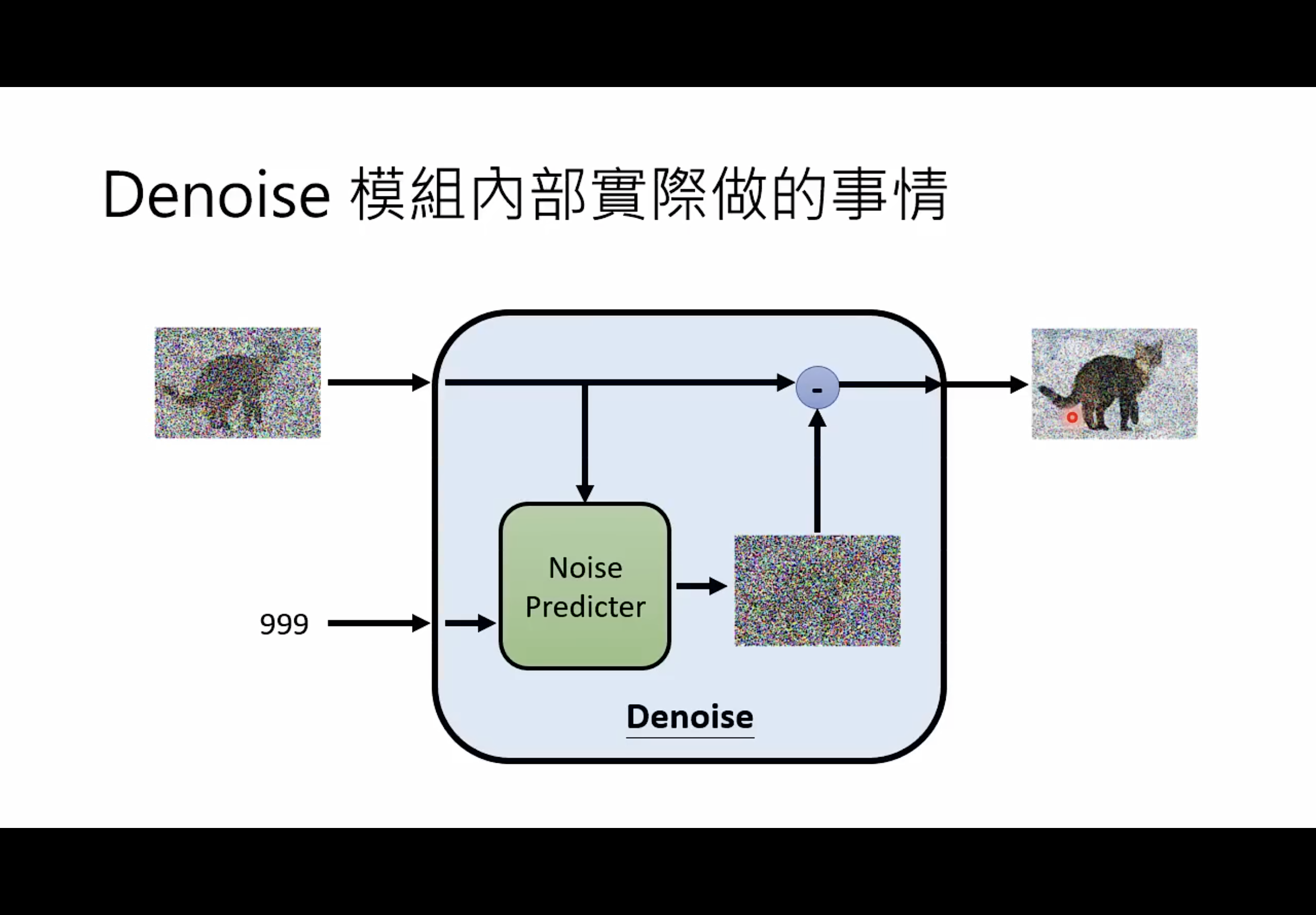
扩散模型的目的是学会如何从Xt中创作一个噪声能稍微少一点的Xt-1。[1] 用噪声预测函数 ${noise’=\epsilon_\theta(x_t, t)}$对模型参数化(即下图的Noise Predictor)。
如果用吴恩达的图片也许会更清晰:
在训练过程中,
- 我们会对原始图片进行逐渐加噪。加噪是利用已知的原始图片X0,现在的时间步t’,和随机噪声 ${\epsilon}$,利用这些来生成Xt。生成的原理是根据下面的式子:
${q(X_t|X_{t-1})=\mathcal N(X_t;\sqrt{1-\beta_t}X_{t-1},\beta_tI)}$
${q_\theta}(X_{1:T}|X_0) = \prod^T_{t=1}q(X_t|X_{t-1})$
- s根据生成的Xt我们利用噪声预测函数对噪声进行反推。显而易见,损失函数就是我们真正的已知的噪声 ${\epsilon}$和预测出的噪声 ${noise’=\epsilon_\theta(x_t, t)}$的差值
${||\epsilon_\theta(x_t, t)-\epsilon||^2}$
训练过程解决了,那我们究竟如何利用噪声预测器对噪声图片采样以获得原始图片呢?也就是上面吴恩达的图片的减号的部分,到底是如何实现的?
实际上在[1]中,作者假设了从Xt到Xt-1的过程也是遵从高斯分布的,即
${p_\theta(X_{t-1}|X_t)=\mathcal N(X_{t-1};\mu_\theta(x_t,t), \Sigma_\theta(x_t,t))}$
其中的平均值mu实际上就可以从噪声预测器的结果获得;而方差是由一个定数决定。因此DM整个的学习过程就是训练噪声预测函数!
资料
原理和代码对照学习:
https://nn.labml.ai/diffusion/ddpm/index.html
[1] Denoising diffusion probabilistic models.