【花书】从概率统计到深度网络的概率预测

参考深度学习花书

第三章概率与信息论【常用统计量，分布】

第五章机器学习基础【参数选择，最大似然估计】

第六章深度前馈网络【输出单元】

概率统计

期望

离散: $E[f(x)]=\sum_xP(x)f(x)$

连续： $E[f(x)]=\int P(x)f(x)dx$

默认地，我们假设E表示对括号内的所有随机变量求平均

性质：线性

$E(af(x)+bg(x)+c)=aE(f(x))+bE(g(x))+c$

方差

对x依照概率分布采样时，随机变量x的函数值会呈现多大的差异

离散： $Var(f(x))=E[(f(x)-E[f(x)])^2]$

协方差

两个变量线性相关性的强度以及这些变量的尺度

$Cov(f(x),g(y))=E[(f(x)-E[f(x)])(g(y)-E[g(y)])]$

随机变量组成的向量之间可构成协方差矩阵，其对角元素为方差

$Cov(x)_{i,j}=Cov(x_i, x_j)$

变量的尺度：1. 绝对值越大，变化越大 2. 若为正，则两个变量都倾向于取较于均值更大的值
相关性：若为0，则无线性相关；若不为0，则一定相关
注意：相关性比独立性的要求更弱。相关性无法判断非线性相关性，而独立性要求线性非线性均无关。

常见分布

伯努利分布

单个二值随机变量的分布。展示了只有两种可能性（0或1）的事件，分别发生的概率x的分布。必然发生的概率为 $\phi$。常用于深度学习的二分类问题。

$P(x=1)=\phi$ $P(x=0)=1-\phi$

将两个式子合二为一：（注意：这个式子只是一种简化写法，并不代表x能取任意值。实际上它只能取{0,1}）

$P(\text{x}=x)=\phi^x(1-\phi)^{1-x}$

其期望和方差：

$E(x)=\phi$ $Var(x)=\phi(1-\phi)$

n重伯努利分布

具有k个不同状态的单个离散型随机变量上的分布。由向量 $p\in\{0,1\}^{k}$ (k个二值元素)参数化。其中每一个分量 $p_i$表示第 $i$个状态的概率。

伯努利分布并不是特别强大，但是它们的领域足够简单。它们可以对那些能够将所有的状态进行枚举的离散型随机变量进行建模。

高斯分布（正态分布）

实数上最常用的分布。由参数 $\mu$和 $\sigma$控制。

$\mathcal N(x;\mu,\sigma^2)=\sqrt{\frac{1}{2\pi \sigma^2}}\text{exp}(-\frac{1}{2\sigma^2}(x-\mu)^2)$

另一种方式是使用 $\beta=1/\sigma^2$来控制分布的精度。写作：

$\mathcal N(x;\mu,\beta^{-1})=\sqrt{\frac{\beta}{2\pi}}\text{exp}(-\frac{1}{2\sigma^2}(x-\mu)^2)$

推广到高维空间的多维正态分布。 $\mu$变为向量表示的均值， $\Sigma$为协方差矩阵（一般写作对角阵即只有方差足矣）

$\mathcal N(x;\mu,\Sigma)=\sqrt{\frac{1}{(2\pi)^n\text{det}(\Sigma)}}\text{exp}(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$ $\mathcal N(x;\mu,\beta^{-1})=\sqrt{\frac{\text{det}(\beta)}{(2\pi)^n}}\text{exp}(-\frac{1}{2}(x-\mu)^T\beta(x-\mu))$

高斯分布具有以下优点：

许多真实事件的分布接近于高斯分布。（中心极限定理）
在相同方差的所有概率分布中，高斯分布具有最大不确定性。因此所需要的先验知识量更少。（少量的训练数据可获得更大的学习收益）

因此正态分布是我们缺乏先验知识时最好的默认选择。

指数分布

x=0周围的边界点的分布。

$\lambda e^{-\lambda x}$ $x \geq 0$
0 $x < 0$

点估计：参数选择与验证

点估计试图为一些感兴趣的参数提供单个最优预测。对于独立同分布的 $\{x^1, x^2…,x^m\}$，点估计或统计量是这些数据的任意函数：

$\hat \theta_m = g(x^1...x^m)$

防止误解，我们一般将真实的参数值写作 $\theta$，将预测值写作 $\hat \theta$

为了衡量预测的点估计的特点，我们一般通过如下性质进行判断

偏差：度量偏离真实参数的误差期望
$bias(\hat \theta_m)=E(\hat \theta_m)-\theta$
方差：度量数据上任意特定采样可能导致的估计期望的偏差
$Var(\hat \theta)$
一致性：估计量的偏离度应随着数据样本的增加而减少
$\text{plim}_{m\rightarrow \infty}\hat \theta_m = \theta$

过拟合与欠拟合

可以看到，两个性质分别对应着参数的不同性质。理想中我们希望两个性质都能最优。实际上，随着模型容量（模型的大小，学习能力）的增大，偏差会降低，方差却会增大，从而进入过拟合的阶段。如何权衡两个值找到最优的模型容量成为重要问题。

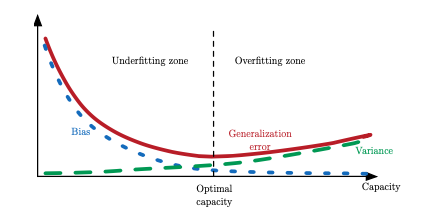
最优模型寻找对策：均方误差与交叉验证

均方误差度量着估计和真实参数间平方误差的总体期望。他同时包含了偏差和方差。因此理想的点估计应该具有较小的MSE。

$\text{MSE}=E[(\hat \theta_m-\theta)^2]=Bias(\hat \theta_m)^2+Var(\hat \theta_m)$

还有一种常见的方法是使用交叉验证对不同模型进行正确评估。最后选择误差最小的模型。

最大似然估计：参数估计

上面讲述了对于得到的参数，如何评判其好坏。本节的最大似然估计则告诉我们如何进行通过数据学习合理的参数。

对参数 $\theta$的最大似然估计为：

（其中 $p_{model}$是模型从数据学到的概率，以估计真实概率 $p_{data}$。真实概率代表了x出现的概率。）

$\theta_{ML}=argmax_{\theta}p_{model}(X,\theta)=argmax_{\theta}\prod^{m}_{i=1} p_{model}(x^i,\theta)=argmax_{\theta}\sum^{m}_{i=1}\log p_{model}=(x^i,\theta)=argmax_{\theta}E_{p\sim \hat p_{data}}\log p_{model}(x^i,\theta)$

不难理解，第一个式子代表了当估计参数能使训练数据x出现概率最大的时候，我们选其为最优参数。之后根据联合概率，log函数的性质，argmax的缩放不变性，变成了最后的式子的样子（为什么是x遵循经验分布下的期望值？因为我们不知道真实分布哇，只能曲线救国咯）。

另一种观点是把最大似然估计看做经验分布和模型分布之间的差异，用KL散度表示（其实也就是交叉熵）：

$$D_{KL}(\hat p_{data}||p_{mdoel})=E_{x\sim \hat p_{data}}[\log \hat p_{data}(x)-\log p_{model}(x)]$

数据相关的统计量我们管不着，因此其实最大似然只和右边的值有关系。

$\theta_{ML}=argmax_{\theta}E_{p\sim \hat p_{data}}\log p_{model}(x^i,\theta)=-E_{x\sim \hat p_{data}}\log p_{model}(x)$

列了一堆式子，最终只要记住上面这一行就够了。所以参数选择中最小化KL散度其实就是等同于最大化似然。

最后，这里的似然估计是对于模拟分布场景的。对于(x,y)类型的监督学习，应该写作：（也就是当数据分布遵循经验分布时，x生成真实值y的概率应该最大）

$\theta_{ML}=-E_{x,y\sim \hat p_{data}}\log p_{model}(y|x)$

输出单元

最后一个问题来了：我们知道了参数如何进行估计，但是最基本的模型分布到底要怎么表示？如何通过数据建模模型分布？这个就涉及到了网络输出层的函数设计：如何使用正确的函数代表 $p_{model}$。

由于网络的任务基本为回归，二分类，多分类。因此只讨论这三种情况下的输出单元。当然，大多数输出单元也可被用于隐藏层。

假设现在神经网络为输出层提供了一组为 $h$的隐藏特征。

线性单元

基于仿射变换。此时假设该线性回归应遵循正态分布。

$\hat y=W^Th+b$ $P(y|x)=\mathcal N (y;\hat y,I)$

sigmoid单元

基于伯努利分布，适用于二分类问题。

$\sigma(x)=\frac{1}{1+\exp(-x)}$

伯努利函数要求变量出现概率应小于1而大于0。sigmoid的性质完美符合了它：

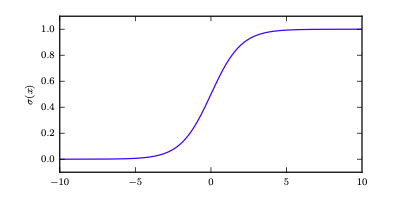
$\sigma(x)=\frac{\exp(x)}{\exp(x)+\exp(0)}$ $\sigma'(x)=\sigma(x)(1-\sigma(x))$ $\sigma(-x)=1-\sigma(x)$

当输入值绝对值较大时，很明显sigmoid的函数将会饱和（很平），这不利于我们计算梯度（非常小）。但是还好，负对数似然会帮我们中和。

softmax单元

基于n重伯努利分布，适用于多分类问题。不仅仅每一个的概率在[0,1]范围内，甚至所有事件的总概率应该是等于1的：

$z = W^Th+b$ $\text{softmax}(z)_i=\frac{\exp(z_i)}{\sum_j{\exp(z_j)}}$

首先线性层进行对数概率的预测，之后再对z进行指数化和归一化（TODO）

太困了，有点匆忙，有空最后再补吧