Colorization using Optimization

论文概述 [1]

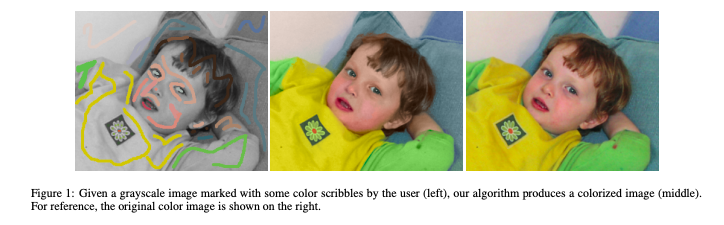
在本文中，我们提出了一种简单的着色方法:基于一个简单前提：时空中具有相似强度(intensity:Y)的相邻像素应该具有相似的颜色。 我们使用次成本函数形式化这个前提，并获得一个可以使用标准技术有效解决的优化问题。

[1]Levin, Anat, Dani Lischinski, and Yair Weiss. “Colorization using optimization.” ACM SIGGRAPH 2004 Papers. 2004. 689-694.

目标函数

Y可以通过gray图像作为已知信息，因此我们需要通过临近像素的推测U和V
MINIMIZE

$$J(U) = \sum_r \left( U(r) - \sum_{s \in N(r)} w_{rs} U(s) \right)^2$$ $$J(V) = \sum_r \left( V(r) - \sum_{s \in N(r)} w_{rs} V(s) \right)^2$$

• r: 目标像素 N(r):临近像素
• $w_{rs}$的条件
  • 两像素间Y越相似，w越大；两像素间Y差值越大，w越小
  • 和为1

约束条件

相邻像素具有相似Y时应该具有相似的U和V

权重函数

$$w_{rs} \propto \exp \left( \frac{-\left(Y(r)-Y(s)\right)^2}{2 \sigma_r^2} \right)$$

• $\sigma_r^2$为包含r的临近像素的variance

实现思路

1. 二乘问题的目的函数转换为解线性方程组Ax=b的问题
   • 如果按照稠密矩阵构造A就需要使用$(A^TA)^{-1}A^Tb$计算，将会十分庞大；如果用稀疏矩阵则会大大减少计算量

     呃呃搞明白以后思路就是如此简单。。。。

代码实现

import库

# 依赖库 
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from skimage import color
from scipy.sparse import csr_matrix
from scipy.sparse.linalg import spsolve

图像预处理

# Load the images
# 打开图片转换为RGB再转换为YUV
img_in   = color.rgb2yuv( np.array( Image.open( 'baby.png' ).convert("RGB"), dtype=float ) / 255 )
img_edit = color.rgb2yuv( np.array( Image.open( 'baby_marked.png' ).convert("RGB"), dtype=float ) / 255 )
img_hint = np.zeros( img_edit.shape )

# 通过图片像素相减提取hint
# 
idx = (np.abs((img_in-img_edit).sum(2)) > 1e-4)
img_hint[ idx ] = img_edit[ idx ]

• Image.open()：返回一个image的对象(shape=(w,h))
  • Image.open().convert("RGB")：返回一个image的RGB对象(shape=(w,h,c))
• sum(n)：沿n维的sum

生成稀疏矩阵A

# Create the optimization problem
w = img_edit.shape[0]
h = img_edit.shape[1]
# window size
wpx = 1 
# u和v：只放入已确定颜色的像素id的uv值
b_u = np.zeros( (w*h,) )
b_v = b_u.copy()
# Sparse matrix，一对(row,col)代表一对邻居关系的像素，dat内存储权重
row = []
col = []
dat = []

# 遍历 w * h = n
for v in range(h):
    for u in range(w):
        # （w，v）to index
        i = v*w + u

        # Add first entry U(r) for both  channels
        # 像素本身等于自身，因此稀疏矩阵A的对角均为1
        row.append( i )
        col.append( i )
        dat.append( 1. )

        # Skip coloured areas,
        # 已经在给的hint里上色的区域就跳过
        if idx[u,v]:
            b_u[i] = img_edit[u,v,1]
            b_v[i] = img_edit[u,v,2]
            continue

        # 求r的neighbour范围
        umin = max(0,u-wpx)
        umax = min(w,u+wpx+1)

        vmin = max(0,v-wpx)
        vmax = min(h,v+wpx+1)
        
        # 求neighbour范围内的variance
        patch = img_in[ umin:umax, vmin:vmax, 0 ]
        mu_r = np.mean( patch )
        sigma_r = np.var( patch )
        sigma_r = max( sigma_r, 1e-6 )
        
        # 求r的Y
        Yr = img_in[u,v,0]

        # Go over neighbours
        # 遍历neighbour，求各自的w
        N = []
        wrs = []
        for nu in range( umin, umax ):
            for nv in range( vmin, vmax ):
                j = nv*w + nu
                if i==j:
                    continue
                Ys = img_in[nu,nv,0]
                wrs.append(np.exp(-1*(Yr-Ys)*(Yr-Ys)/ 2 / sigma_r))
                N.append(j)
        wrs = np.array( wrs )
        # 对w的约束条件：和必须为1
        wrs /= wrs.sum()

        # 根据求出的w完善矩阵
        for k,j in enumerate(N):
            row.append(i)
            col.append(j)
            dat.append(-wrs[k])

# 最终生成一个大小为(wh,wh)的，包含所有点与点之间的权重的矩阵
A = csr_matrix( (dat, (row,col)) )

• csr_matrix( (data, (row_index,col_index)) ):

  csr_matrix( ([1,2,1], ([1,3,3],[0,1,3])) ).toarray()
  
  >>> array([[0, 0, 0, 0],
     [1, 0, 0, 0],
     [0, 0, 0, 0],
     [0, 2, 0, 1]], dtype=int64)

解方程组生成目标图像

# Solve the optimization and display results
Y = img_in[:,:,0:1]
U = spsolve(A, b_u).reshape( h, w, 1 ).transpose( (1,0,2) )
V = spsolve(A, b_v).reshape( h, w, 1 ).transpose( (1,0,2) )

img_out = np.concatenate( (Y,U,V), axis=2 )
plt.imshow( color.yuv2rgb(img_out) )
plt.show()